Van Hiele Levels

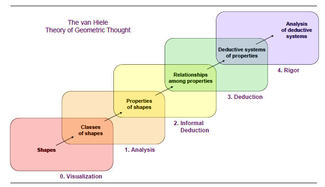
In class this week we discussed and practiced the Van Hiele Levels. In the 1950s, a husband and wife team of Dutch educators, Pierre van Hiele and Diana van Miele-Geldof, developed a theory of how children learn geometry which is still widely accepted today. Through their research, they identified five levels of understanding through which children move sequentially on their way towards geometric thinking. 
Level 0- (Visualization). The student reasons about basic geometric concepts, such as simple shapes, primarily by means of visual considerations of the concept as a whole without explicit regret to properties of its components.
Level 1- (Analysis). The student reasons about geometric concepts by means of an informal analysis of component parts and attributes. Necessary properties of the concept are established.
Level 2- (Abstraction). The student logically orders the properties of concepts, forms abstract definitions, and can distinguish between the necessity and sufficiency of a set of properties in determining a concept.
Level 3- (Deduction). The student reasons formally within the context of a mathematical system, complete with undefined terms, axioms, and underlying logical system, definitions and theorems.
Level 4- (Rigor). The student can compare systems based on different axioms and can study various geometries in the absence of concrete models.
Every teacher needs to learn how to understand our learners, and understand what questions to ask to help move students to the next level. Although we are always passing though the levels, typically grades K-8 are in levels 0-2. Watching students move through these levels is when they are understanding for example that a square is a square but that a square is also a rectangle. 
I read the article "Developing Geometric Thinking through Activities That Begin with Play" and I can't help but think about when know when to start moving your students through these levels. I read on and discover that this all depends on the students'  level of thinking. This makes all the sense in the world because how can you teach a student at a level farther then they have mastered. 

---